目标
- 掌握计算图的原理
- 掌握计算图静态生成和动态生成算法
- 掌握计算图的常用执行方法
什么是计算图?
计算图(Computational Graph)是机器学习和深度学习中用于表示计算过程的一种数据结构。它由节点(Node)和边(Edge)组成,其中节点操作(例如:加法、乘法、激活函数等),边表示张量的状态及张量之间的依赖关系,即数据流动的方向。
计算图在深度学习框架中作用包括:
- 统一的计算过程表达:在编写机器学习模型程序的过程中,用户希望使用高层次编程语言(如Python、Julia和C++)。然而,硬件加速器等设备往往只提供了C和C++编程接口,因此机器学习系统的实现通常需要基于C和C++。用不同的高层次语言编写的程序因此需要被表达为一个统一的数据结构,从而被底层共享的C和C++系统模块执行。这个数据结构(即计算图)可以表述用户的输入数据、模型中的计算逻辑(通常称为算子)以及算子之间的执行顺序。
- 自动微分:通过计算图可以自动计算梯度,简化了手动推导和编码梯度的过程。
- 优化性能:计算图可以优化计算过程,例如通过融合操作来减少内存消耗和计算时间。
- 可视化:计算图可以帮助我们理解模型的结构和数据流动,便于调试和优化。
在实际应用中,如TensorFlow、PyTorch等深度学习框架都使用计算图来构建和训练模型。用户可以通过定义计算图来构建模型,然后利用框架提供的优化器和反向传播算法来训练模型。
计算图的基本构成
如使用计算图表示\(Z=ReLU(X*Y)\) 则可使用如下的计算图表示
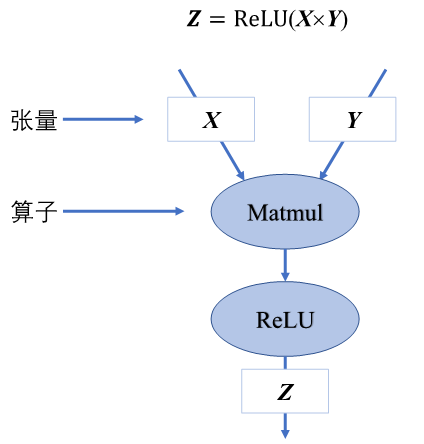
张量
张量作为基本数据结构,具有如下属性:
| 属性 | 功能 | 实例 |
|---|---|---|
| 秩或维数 | 表示张量的轴数 | 标量为0,向量为1,矩阵为2... |
| 形状(shape) | 张量每个维度的长度 | 如[3,3,3] |
| 数据类型(dtype) | 张量存储的数据类型 | bool、uint8、int16、float32、float64等,默认为float32 |
| 存储位置 | 创建张量时可以指定存储的设备位置 | CPU、GPU |
| 名字 | 张量的标识符 | 略 |
以下为部分张量的可视化:
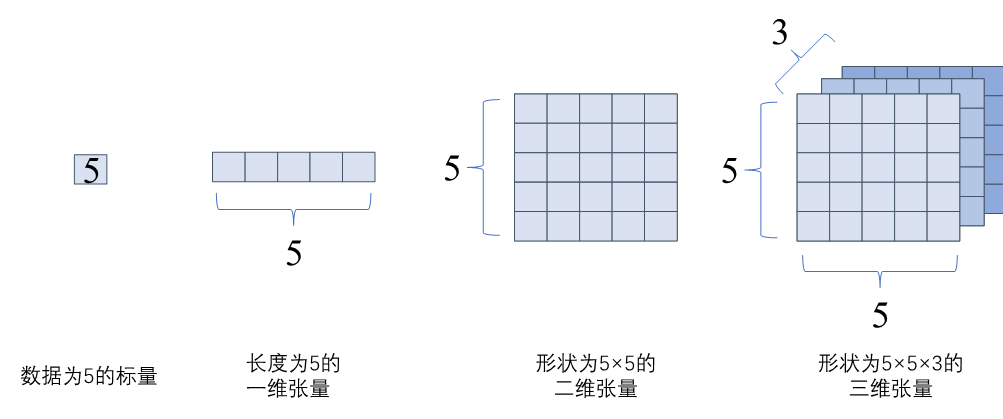
算子
算子是计算图基本计算单元,对张量数据进行加工处理,我们按照功能将算子分为以下四个类别:
- 张量操作算子:包括张量的结构操作和数学运算。
- 神经网络算子:包括特征提取、激活函数、损失函数、优化算法等。
- 数据流算子:包括数据的预处理和数据载入相关算子,数据预处理主要针对图像的裁剪填充、旋转、归一化等;数据载入算子包括对数据集的随机乱序、分批载入、预载入等。
- 控制流算子:可以控制计算图的数据流向,如条件运算符和循环运算符。控制流操作不仅会影响神经网络模型的前向运算,也会影响反向梯度计算。
依赖计算
计算图是一个有向无环图。如果表示如下的代码:
1 | y1 = relu(matmul(X1, W1)) |
可以使用如下计算图:
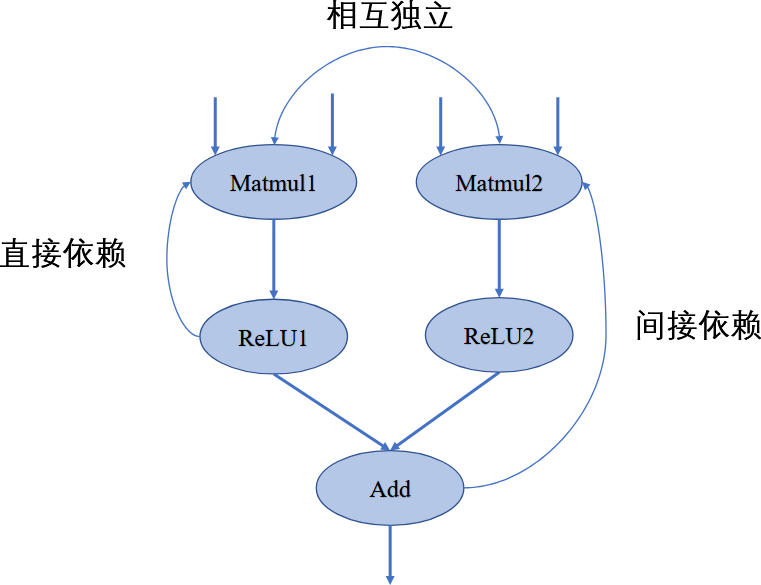
将依赖关系进行区分如下:
- 直接依赖:节点ReLU1直接依赖于节点Matmul1,即如果节点ReLU1要执行运算,必须接受直接来自节点Matmul1的输出数据;
- 间接依赖:节点Add间接依赖于节点Matmul1,即节点Matmul1的数据并未直接传输给节点Add,而是经过了某个或者某些中间节点进行处理后再传输给节点Add,而这些中间节点可能是节点Add的直接依赖节点,也可能是间接依赖节点;
- 相互独立:在计算图中节点Matmul1与节点Matmul2之间并无数据输入输出依赖关系,所以这两个节点间相互独立。
循环关系
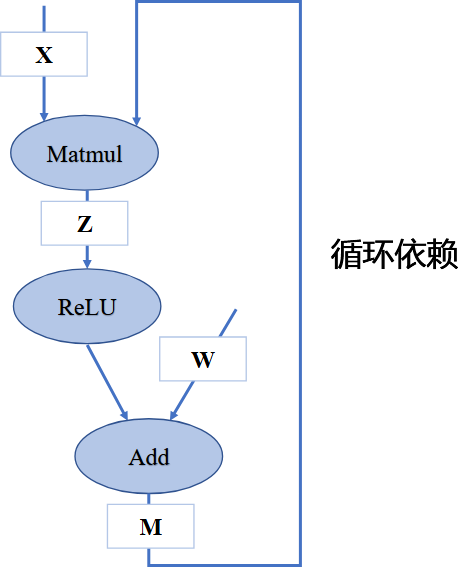
循坏依赖问题
若我们手动同时给两个节点赋予输入,计算将持续不间断进行,模型训练将无法停止造成死循环。在构建深度学习模型时,应避免算子间产生循环依赖。
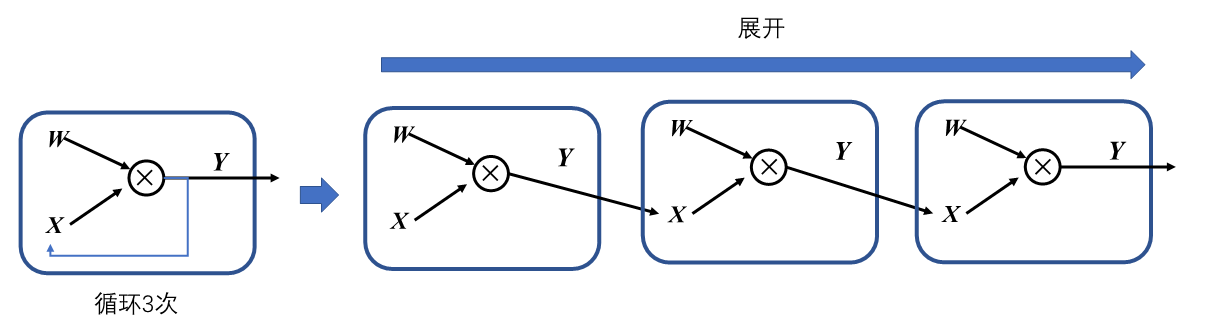
展开机制
在机器学习框架中,表示循环关系(Loop Iteration)通常是以展开机制(Unrolling)来实现。循环三次的计算图进行展开如下图。循环体的计算子图按照迭代次数进行复制3次,将代表相邻迭代轮次的子图进行串联,相邻迭代轮次的计算子图之间是直接依赖关系。
控制流
控制流主要包括循环和分支,在模型中引入控制流后可以让计算图中某些节点循环执行任意次数,也可以根据条件判断选择某些节点不执行。
目前主流的机器学习框架中通常使用两种方式来提供控制流:
- 使用高级编程语言(图外方法,Out-of-Graph Approach):图外方法允许用户直接使用if-else、while和for这些Python命令来构建控制流。该方法使用时灵活易用便捷直观。
- 使用机器学习框架控制原语(图内方法,In-Graph Approach):TensorFlow中可以使用图内方法控制流算子(如tf.cond条件控制、tf.while_loop循环控制和tf.case分支控制等)来构建模型控制流,这些算子是使用更加低级别的原语运算符组合而成。图内方法的控制流表达与用户常用的编程习惯并不一致,牺牲部分易用性换取的是计算性能提升。
条件控制计算图的正向传播与反向传播
在下例中,应用了简单的条件控制:
1 | def control(A, B, C, conditional = True): |
下图描述了条件控制代码的前向计算图和反向计算图:
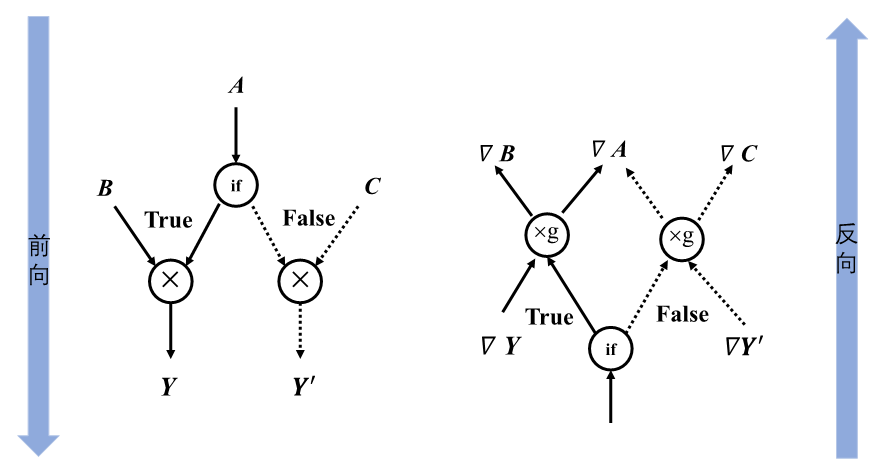
如果在前向传播过程中,张量\(C\)经过条件控制,不参与运算,那么在反向传播过程中,同样不会计算\(C\)的梯度
循环控制计算图的正向传播与反向传播
在下例中,应用了简单的循环控制:
1 | def recurrent_control(X : Tensor, W : Sequence[Tensor], cur_num = 3): |
将循环展开后,计算图如下:
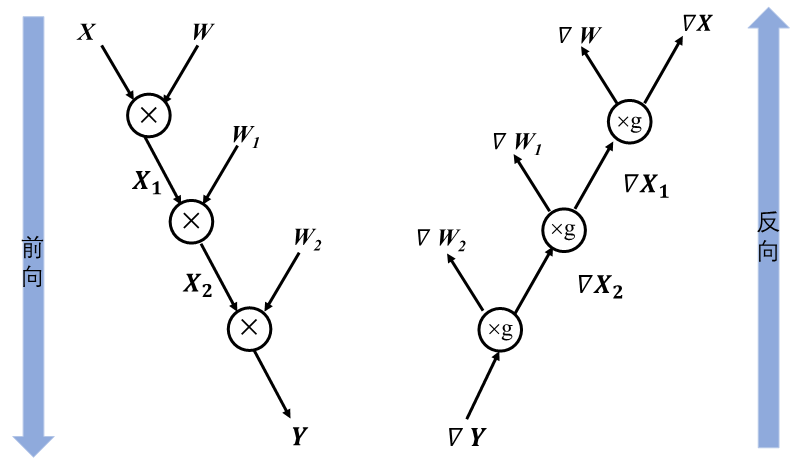
循环控制的梯度反向传播同样也是一个循环,它与前向循环的迭代次数相同。
基于链式法则的梯度计算
计算图的方向
举例:对于函数\(y=f(x)\)来说,有如下计算图:
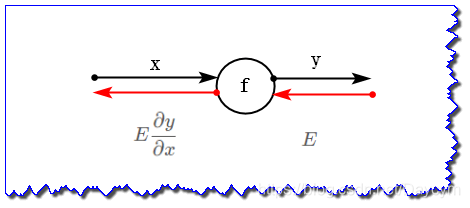
其中,黑色代表正向传播,红色代表反向传播。对于反向传播,有如下计算顺序:
- 将信号\(E\)乘以节点的局部导数\(\frac{\partial y}{\partial x}\)
- 传递给下一个节点。
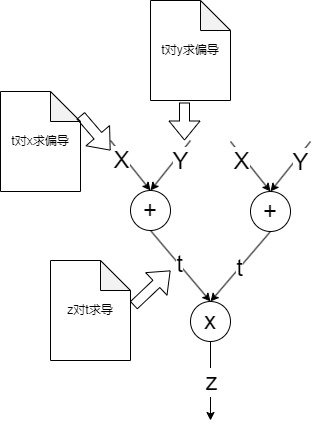
链式法则的梯度计算
那我们再看一个稍显复杂的反向传播。
\[ t=x+y \\ z=t^2 \]
绘制计算图如下: